這一節(jié)課，小編要講講數(shù)學(xué)，大家認(rèn)真讀。數(shù)學(xué)，算是所有科目中比較難學(xué)的一個(gè)科目，估計(jì)很多同學(xué)對(duì)數(shù)學(xué)是深惡痛絕！

你發(fā)現(xiàn)沒(méi)有，對(duì)有些人卻不一樣（我們不一樣，不一樣！），他們一點(diǎn)都不覺(jué)得數(shù)學(xué)難學(xué)，反而覺(jué)得它很有趣。為了證明數(shù)學(xué)的有趣，小編給大家舉個(gè)例子：

那么繼續(xù)：

那接下來(lái)，有趣的事情發(fā)生了：

大家看到?jīng)]？相等了。不是1≈0.999999…嗎？怎么變成了相等？

關(guān)于1=0.999999……還是1≈0.999999……，這兩個(gè)之間，到底是怎么回事？……好吧，小編也不能給出解釋。

目前，對(duì)于這個(gè)問(wèn)題，自然界有兩個(gè)相反的說(shuō)法，一個(gè)是0.999999循環(huán)，在自然界中，是根本不存在的，宇宙中沒(méi)有任何一個(gè)實(shí)際物體，具有0.99...99這個(gè)數(shù)值……

另外一個(gè)猜測(cè)是：1的無(wú)窮次方等于1；而0.9999.....的無(wú)窮次方等于0，所以兩者不相等……

很顯然，這兩個(gè)都是符合我們?nèi)缃竦臄?shù)學(xué)認(rèn)知，而且還相互矛盾的！這就更加讓人難以明白，到底是等于，還是約等于，還是差距非常大！

這算是數(shù)學(xué)的一個(gè)悖論！但是！現(xiàn)在不明白，不等于以后不明白！數(shù)學(xué)，是一個(gè)發(fā)展的學(xué)科！

小編在這里，跟大家分享一下，數(shù)學(xué)的三次危機(jī)，都是因?yàn)閿?shù)學(xué)發(fā)展過(guò)程中不夠完善，差點(diǎn)斷送了數(shù)學(xué)這個(gè)學(xué)科。

在公元前五世紀(jì)以前，數(shù)學(xué)學(xué)科畢達(dá)哥拉斯學(xué)派主張【“數(shù)”是萬(wàn)物的本原、始基】，而宇宙中一切現(xiàn)象都可歸結(jié)為整數(shù)或整數(shù)之比，有理數(shù)理論成為占統(tǒng)治地位的數(shù)學(xué)規(guī)范……

畢達(dá)哥拉斯

小編這里先復(fù)習(xí)一下【有理數(shù)】的概念，它是整數(shù)（正整數(shù)、0、負(fù)整數(shù)）和分?jǐn)?shù)的統(tǒng)稱。這個(gè)有理數(shù)，是那個(gè)時(shí)候的數(shù)學(xué)的理論基石，不可動(dòng)搖。

結(jié)果，在公元前580～568年間，一個(gè)畢達(dá)哥拉斯學(xué)派內(nèi)部的一個(gè)成員希帕索斯，有一天突然發(fā)現(xiàn)：邊長(zhǎng)為1的正方形的對(duì)角線長(zhǎng)度（根號(hào)2）既不是整數(shù)，也不能用整數(shù)之比來(lái)表示。

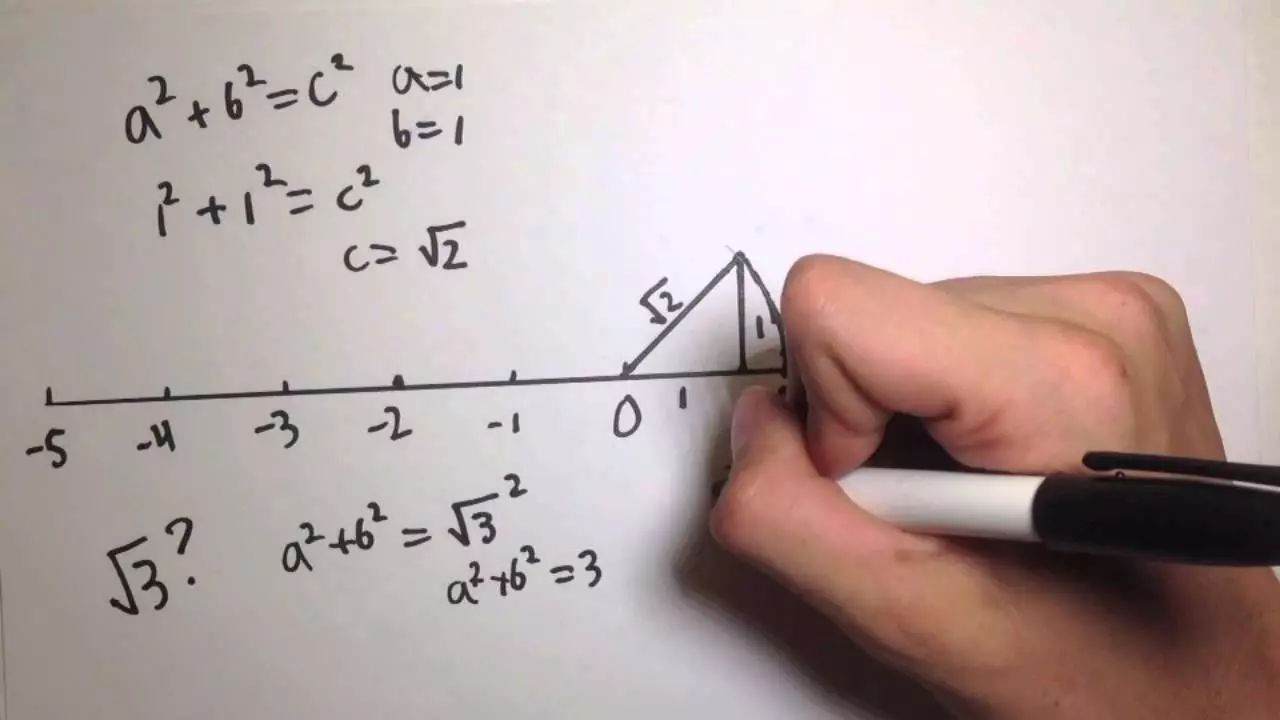
這一發(fā)現(xiàn)不僅嚴(yán)重觸犯了畢達(dá)哥拉斯學(xué)派的信條，同時(shí)也沖擊了當(dāng)時(shí)希臘人的普遍見解，因此它直接導(dǎo)致了數(shù)學(xué)認(rèn)識(shí)上的“危機(jī)”，動(dòng)搖到了數(shù)學(xué)的根基。

這一悖論導(dǎo)致了Hipasus被畢達(dá)哥拉斯學(xué)派追殺，最終葬身大海的悲劇。

希帕索斯的這一發(fā)現(xiàn)，史稱“希帕索斯悖論”，從而觸發(fā)了第一次數(shù)學(xué)危機(jī)。

也正是因?yàn)檫@次數(shù)學(xué)悖論的出現(xiàn)，證明了人的直覺(jué)和經(jīng)驗(yàn)不一定靠得住，而推理和證明才是可靠的，這就導(dǎo)致了亞里士多德的邏輯體系和歐幾里德幾何體系的建立……

過(guò)了兩百年，希臘數(shù)學(xué)家歐多克斯和阿契塔斯兩人給出了“兩個(gè)數(shù)的比相等”的新定義，建立起一套完整的比例論，其中巧妙避開了無(wú)理數(shù)這一“邏輯上的丑聞”，并保留住與之相關(guān)的一些結(jié)論，緩解了這次數(shù)學(xué)危機(jī)。

然而，“世界萬(wàn)物皆為整數(shù)或整數(shù)比”的錯(cuò)誤并沒(méi)有解決，歐多克斯只是借助幾何方法，直接避免無(wú)理數(shù)的出現(xiàn)。

直到1872年，德國(guó)數(shù)學(xué)家對(duì)無(wú)理數(shù)作出了嚴(yán)格的定義，無(wú)理數(shù)本質(zhì)被徹底搞清，無(wú)理數(shù)在數(shù)學(xué)中合法地位的確立，才真正徹底、圓滿地解決了第一次數(shù)學(xué)危機(jī)。

好了，這個(gè)第一次數(shù)學(xué)危機(jī)就講到這里，回到1=0.999999……還是1≈0.999999……這個(gè)問(wèn)題上來(lái)，就像這個(gè)根號(hào)2的出現(xiàn)動(dòng)搖了當(dāng)時(shí)的數(shù)學(xué)體系的情況一樣，不相信根號(hào)2的存在……

而現(xiàn)在，有人不相信0.9999……無(wú)限循環(huán)不存在，不用擔(dān)心，當(dāng)未來(lái)數(shù)學(xué)發(fā)展到一定的程度時(shí)，它就存在了，也許到時(shí)候，會(huì)出現(xiàn)一個(gè)新的數(shù)學(xué)概念，1=0.999999……還是1≈0.999999這個(gè)問(wèn)題，就像是當(dāng)初的【無(wú)理數(shù)】概念一樣……

17世紀(jì)末，牛頓和萊布尼茨分別獨(dú)立地建立了微積分方法，成為解決眾多問(wèn)題的重要而有力的工具，并在實(shí)際應(yīng)用中獲得了巨大成功。

微積分是初等和高等數(shù)學(xué)的分水嶺。萊布尼茨說(shuō)：從人類有數(shù)學(xué)開始到牛頓時(shí)代，牛頓的貢獻(xiàn)至少一半以上！盡管如此，從本質(zhì)上說(shuō)，還是科學(xué)技術(shù)的發(fā)展催生了微積分 。

17世紀(jì)，科學(xué)技術(shù)發(fā)展迅猛，向數(shù)學(xué)提出四類問(wèn)題：瞬時(shí)速度問(wèn)題；曲線的切線問(wèn)題；函數(shù)極值問(wèn)題；曲線長(zhǎng)度和圖形面積問(wèn)題。以上四類問(wèn)題吸引了大批數(shù)學(xué)家，產(chǎn)生了新的數(shù)學(xué)工具：坐標(biāo)解析幾何。

微積分的建立標(biāo)志著數(shù)學(xué)從常數(shù)數(shù)學(xué)時(shí)代進(jìn)入變數(shù)數(shù)學(xué)時(shí)代，推動(dòng)了整個(gè)科學(xué)技術(shù)的發(fā)展。

然而，微積分學(xué)產(chǎn)生伊始，迎來(lái)的并非全是掌聲，在當(dāng)時(shí)它還遭到了許多人的強(qiáng)烈攻擊和指責(zé)，原因在于當(dāng)時(shí)的微積分主要建立在無(wú)窮小分析之上，而無(wú)窮小后來(lái)證明是包含邏輯矛盾的。

1734年愛(ài)爾蘭主教貝克萊提出貝克萊悖論：無(wú)窮小量 dx 既是0又不是0！

無(wú)窮小量究竟是不是零？無(wú)窮小及其分析是否合理？這引起了數(shù)學(xué)界甚至哲學(xué)界長(zhǎng)達(dá)一個(gè)半世紀(jì)的爭(zhēng)論。

如果解不到這個(gè)問(wèn)題，所謂無(wú)堅(jiān)不摧的微積分，便無(wú)立足之地，一切由微積分所得出來(lái)的完美的數(shù)學(xué)和物理學(xué)上的結(jié)果也付諸流水，所以數(shù)學(xué)史上稱之為“第二次數(shù)學(xué)危機(jī)”。

 數(shù)學(xué)是講究嚴(yán)謹(jǐn)?shù)膶W(xué)科，數(shù)學(xué)家必不逃避問(wèn)題，面對(duì)困難，接受挑戰(zhàn)，是數(shù)學(xué)家的不朽格言。

化解這一悖論的重大科學(xué)發(fā)現(xiàn)是極限論，它使得微積分得以嚴(yán)密化。

1820年，另一位偉大的數(shù)學(xué)家柯西（1789–1857），重新建立微積分學(xué)的基礎(chǔ)——數(shù)學(xué)分析。

數(shù)學(xué)分析是透過(guò)一套嚴(yán)格的“數(shù)學(xué)語(yǔ)言——ε–語(yǔ)言”來(lái)說(shuō)明甚么是變量、無(wú)窮小和極限等的概念和定義，解決了甚么是既不是零又不是非零的問(wèn)題，而這次的危機(jī)亦安然渡過(guò)，并為數(shù)學(xué)的大家庭增添了一位成員“數(shù)學(xué)分析”。

魏爾斯托拉斯進(jìn)一步改進(jìn)柯西的工作，給出極限的 e--d 語(yǔ)言定義：

經(jīng)過(guò)數(shù)位杰出數(shù)學(xué)家對(duì)于微積分學(xué)基礎(chǔ)概念的重建后，第三次數(shù)學(xué)危機(jī)才終于得以解決。

19世紀(jì)后期，高等數(shù)學(xué)（微積分），線性代數(shù)（多項(xiàng)式，矩陣，行列式），幾何學(xué)（射影幾何）已經(jīng)發(fā)展得十分完備； 

一些新的數(shù)學(xué)分支，如泛函分析，抽象代數(shù)，拓?fù)鋵W(xué)，等等，開始出現(xiàn)；

康托建立了集合論-----現(xiàn)代數(shù)學(xué)的基礎(chǔ)。

1900年龐加萊稱：數(shù)學(xué)的嚴(yán)格性，看來(lái)直到今天才可以說(shuō)是實(shí)現(xiàn)了。正在此時(shí)，羅素定義的集合R：所有不以自己為元素的集合所組成的集合R = { x | x ? x } 。

這個(gè)漏洞就源于英國(guó)數(shù)學(xué)家羅素提出的一個(gè)悖論：所有不包含自身的集合的集合，它到底包不包含自身呢？如果它包含自身，那么它就不是不包含自身的集合，所以也就不是所有不包含自身的集合的集合的元素。

伯特蘭·羅素(Bertrand Russell，1872.5.18-1970.2.2)

如果它不包含自身，那它理應(yīng)是所有不包含自身的集合的集合的一個(gè)元素。這樣的一個(gè)集合，包不包含自身，都必將引發(fā)矛盾。

對(duì)于羅素悖論，有一個(gè)通俗的故事可以解釋，就是“理發(fā)師悖論”。

羅素悖論一經(jīng)提出便在當(dāng)時(shí)的數(shù)學(xué)界與邏輯學(xué)界內(nèi)引起了軒然大波，直接導(dǎo)致了第三次數(shù)學(xué)危機(jī)！

弗雷格（Friedrich Ludwig Gottlob Frege，1848.11.8-1925.7.26)

由于這個(gè)悖論，費(fèi)雷格的著作《算術(shù)原理》中的第五公理竟然是錯(cuò)的！他感覺(jué)算術(shù)的基礎(chǔ)發(fā)生了動(dòng)搖。

最后只能在自己著作的末尾寫道：“一個(gè)科學(xué)家所碰到的最倒霉的事，莫過(guò)于是在他的工作即將完成時(shí)卻發(fā)現(xiàn)所干的工作的基礎(chǔ)崩潰了。”

那么，這次危機(jī)是如何得到解決的呢？

事實(shí)上，為了解決羅素悖論，演化出邏輯主義，直覺(jué)主義，形式主義等數(shù)學(xué)學(xué)派，產(chǎn)生了集合論的公理化。人們注意到，必須對(duì)康托的樸素集合論加以限制，限制到足以排除悖論，同時(shí)保留所有有價(jià)值的東西。 

龐加萊說(shuō)，我們建造了一個(gè)圍欄來(lái)放養(yǎng)羊群，以防止它們被狼侵害，但我們不知道在圍欄中是否已經(jīng)有狼。

直到1931年，哥德爾提出了一系列不完備定理并予以證明：

至此，這場(chǎng)關(guān)于數(shù)學(xué)基礎(chǔ)的爭(zhēng)論終于結(jié)束，同時(shí)也宣告了把數(shù)學(xué)徹底形式化的愿望是不可能實(shí)現(xiàn)的。

數(shù)學(xué)是講究嚴(yán)謹(jǐn)?shù)膶W(xué)科，數(shù)學(xué)家必不逃避問(wèn)題，面對(duì)困難，接受挑戰(zhàn)，是數(shù)學(xué)家的不朽格言。

歷史上的三次數(shù)學(xué)危機(jī)，雖然給人們帶來(lái)了極大的麻煩，但是危機(jī)的產(chǎn)生使人們認(rèn)識(shí)到了現(xiàn)有理論的缺陷，并不斷去完善，由此，數(shù)學(xué)也會(huì)得到新的發(fā)展，甚至?xí)懈锩缘牡淖兏铮?/span>

事實(shí)上，悖論的產(chǎn)生往往預(yù)示著科學(xué)的發(fā)展，可以說(shuō)，悖論是科學(xué)發(fā)展的產(chǎn)物，是科學(xué)發(fā)展源泉之一。

第一次數(shù)學(xué)危機(jī)使人們發(fā)現(xiàn)無(wú)理數(shù)，建立了完整的實(shí)數(shù)理論，歐氏幾何也應(yīng)運(yùn)而生并建立了幾何公理體系；

第二次數(shù)學(xué)危機(jī)的出現(xiàn)，直接導(dǎo)致了極限理論、實(shí)數(shù)理論和集合論三大理論的產(chǎn)生和完善，使微積分建立在穩(wěn)固且完美的基礎(chǔ)之上；

第三次數(shù)學(xué)危機(jī),使集合論成為一個(gè)完整的集合論公理體系（ZFC系統(tǒng)）,促進(jìn)了數(shù)學(xué)基礎(chǔ)研究及數(shù)理邏輯的現(xiàn)代性。